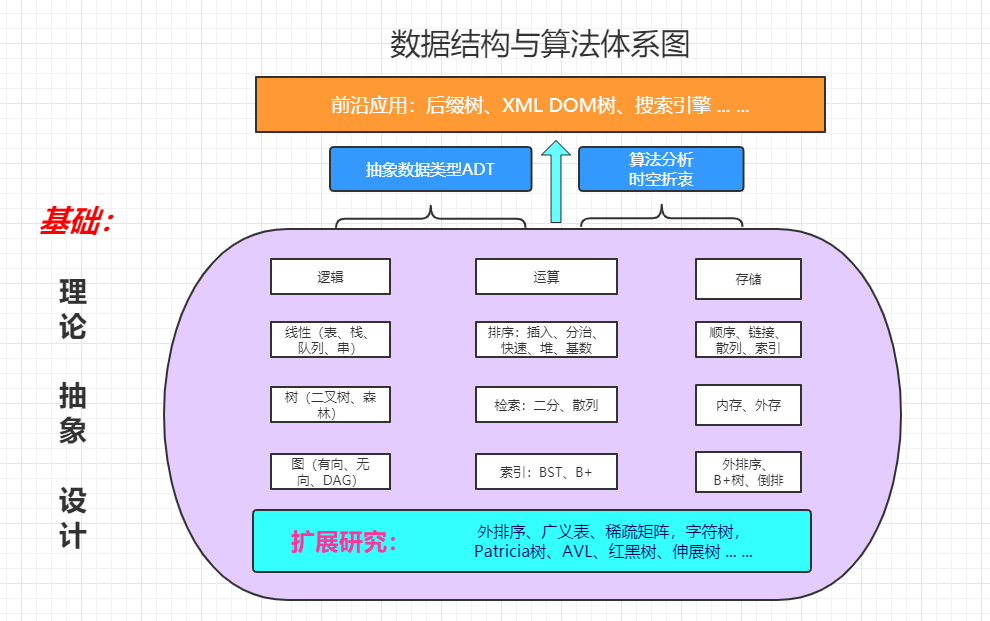
# 基本的数据结构
# 认识数据结构
# 数据结构的说明
数据结构起源于程序设计,是用计算机来存储、组织数据的方式。数据结构不是使我们学会编码,而是为我们提供一种编程的思想,具有更好的思路。
关于数据结构有两种说法,如下:
- 广义的说法:数据结构 = 数据存储 + 算法
- 狭义的说法:数据结构 = 数据的存储;
# 数据结构和算法的关系
数据结构与算法是相互依托的关系。计算机解决问题,应该是先从具体问题中抽象出一个适当的数据模型,设计出一个解此数据模型的算法:
- 数据结构 ==> 建筑工程中的建筑设计图
- 算法 ==> 工程中的施工流程图
# 用数据结构可以做什么
- 程序员的内功心法之一
- 有效管理数据对象
- 解决处理性能问题
- 面试加分项(现在一些简单的数据结构和算法已经是必备项了)
# 基本数据结构及衍生结构
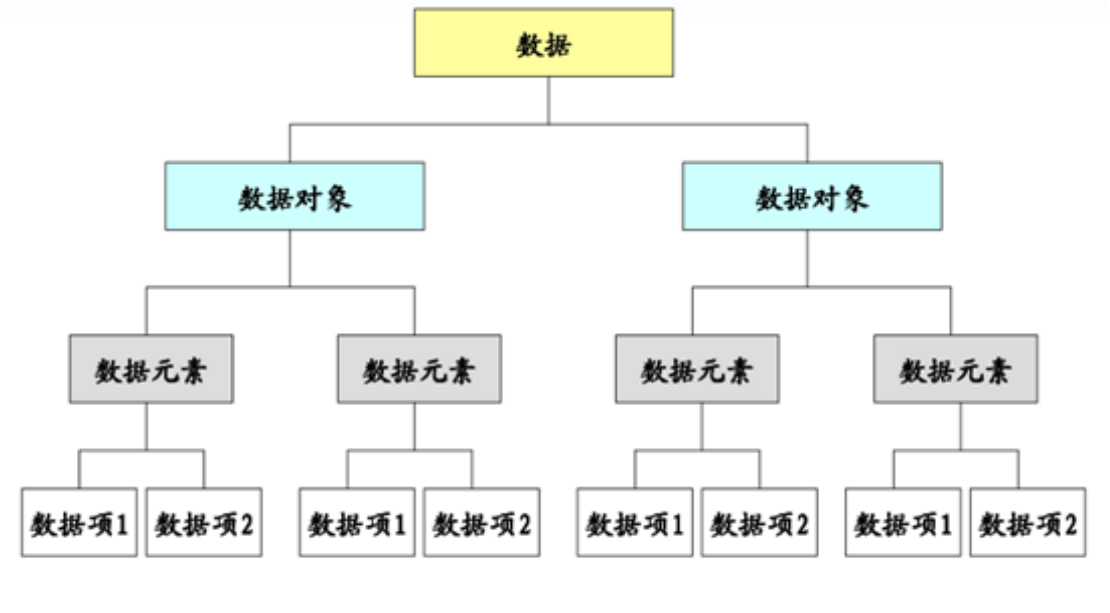
# 几个算法中的基本概念
- 数据
- 数据元素
- 数据项
- 数据对象
- 数据结构
它们之间的关系就像下图一样:
# 浅析数据结构
数据元素相互之间的关系称为结构。数据结构是与算法紧密结合的。
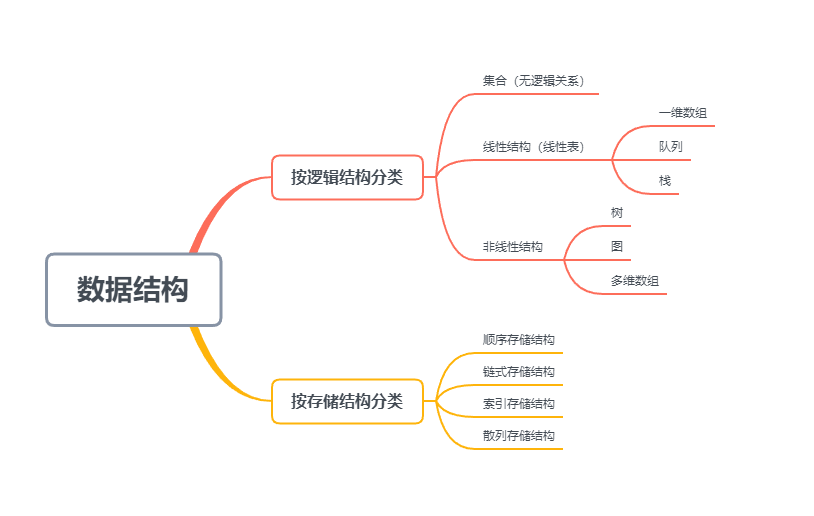
- 逻辑结构:反映数据元素之间的逻辑关系。
- 存储结构:数据结构在计算机中的表示。
- 算法:对数据的操作
# 基本的逻辑结构
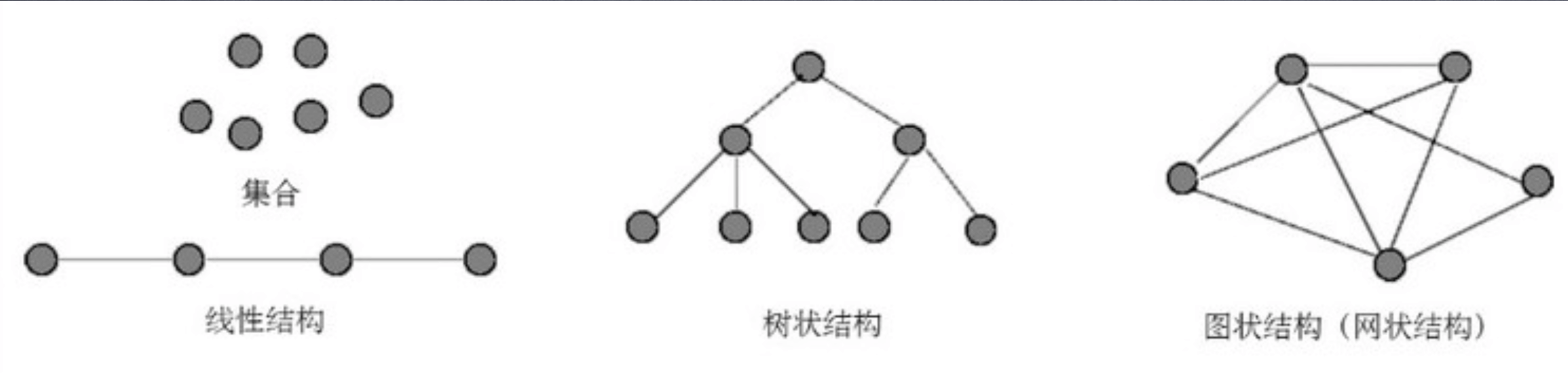
- 集合
- 线性结构
- 树状结构
- 图状结构(网状结构)
# 集合
数据结构中的集合关系就类似于数学中的集合。
- 集合中的数据成员是无序的。
- 每个数据成员在集合中不能重复,仅且只出现一次。
# 线性表
线性结构中的数据元素之间是一对一的关系。也就是数据元素一个接一个地排列。
- 用来存放特定的某一个类型的元素
- 物理结构为顺序表和链表
- 线性表的基本操作
- 1.创建线性表
- 2.添加元素
- 3.删除元素
- 4.读数据
- 5.遍历线性表
- 6.查找线性表
- 7.销毁线性表
# 线性表的衍生结构
- 1.栈
- 2.队列
- 3.串
- ...
# 栈
栈是一种被限制操作的线性表。栈是一种先进后出 LIFO(Last In First Out) 的数据结构。(桶装的薯片是现实中一个最简单的栈结构))
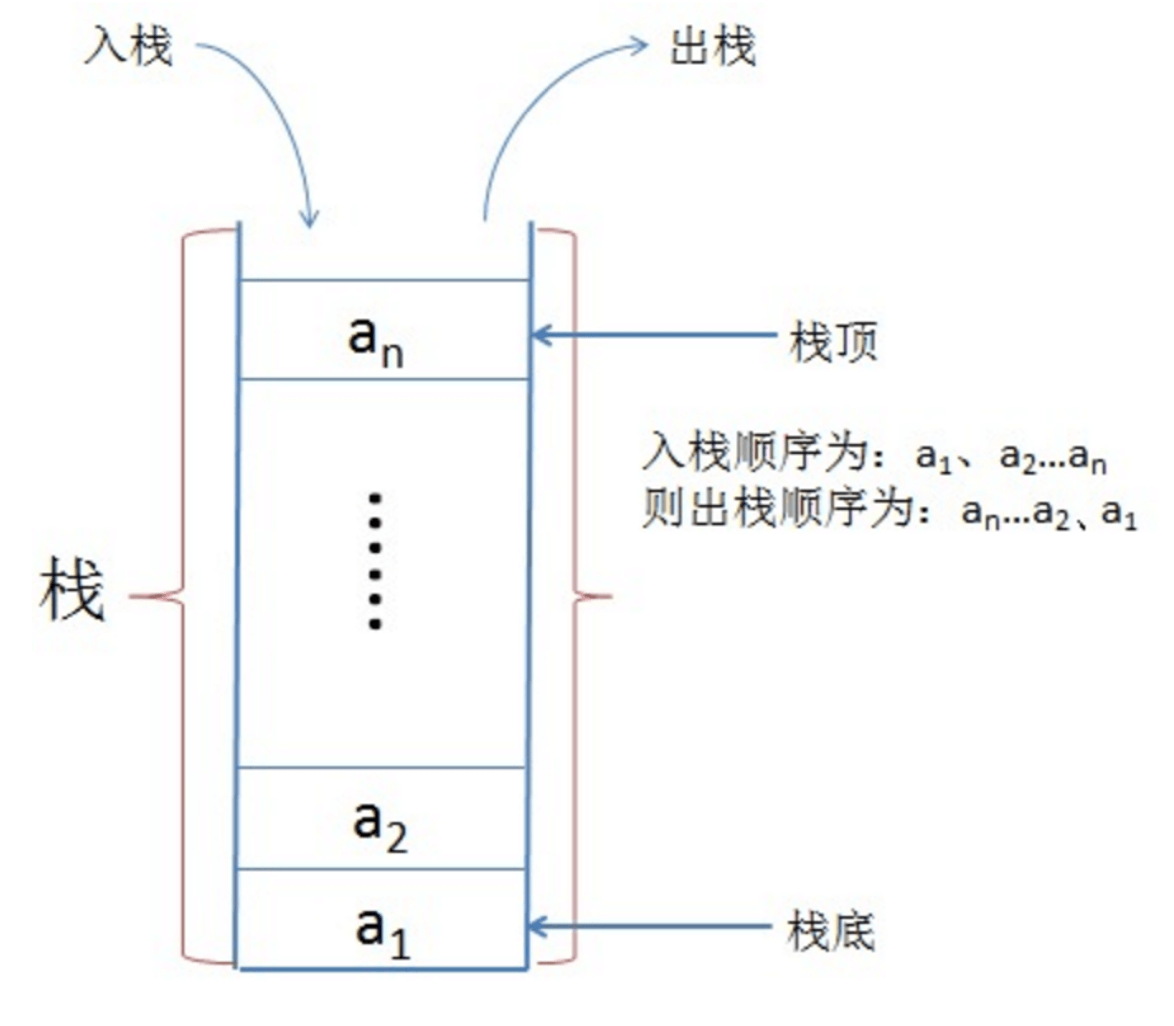
基本概念
- 向栈中添加数据叫入栈
- 从栈中向外拿数据叫出栈
- 栈中没有数据叫空栈
- 空栈或者栈中只有1个元素的时候 栈顶即是栈底
- 添加元素的时候,栈顶在不断的变化
操作规则
- 创建栈结构
- 入栈
- 出栈
- 读栈顶
- 清空栈
- 销毁栈结构
用途:
- 解决括号匹配检查
- 浏览器的后退或编辑器的undo功能
# 队列
队列是一种被限制操作的线性表。队列是一种先进先出 FIFO(First In First Out) 的数据结构。(我们在吃自助的时候,放冰淇凌筒的那个管子就是一种队列,只能从上往下走)
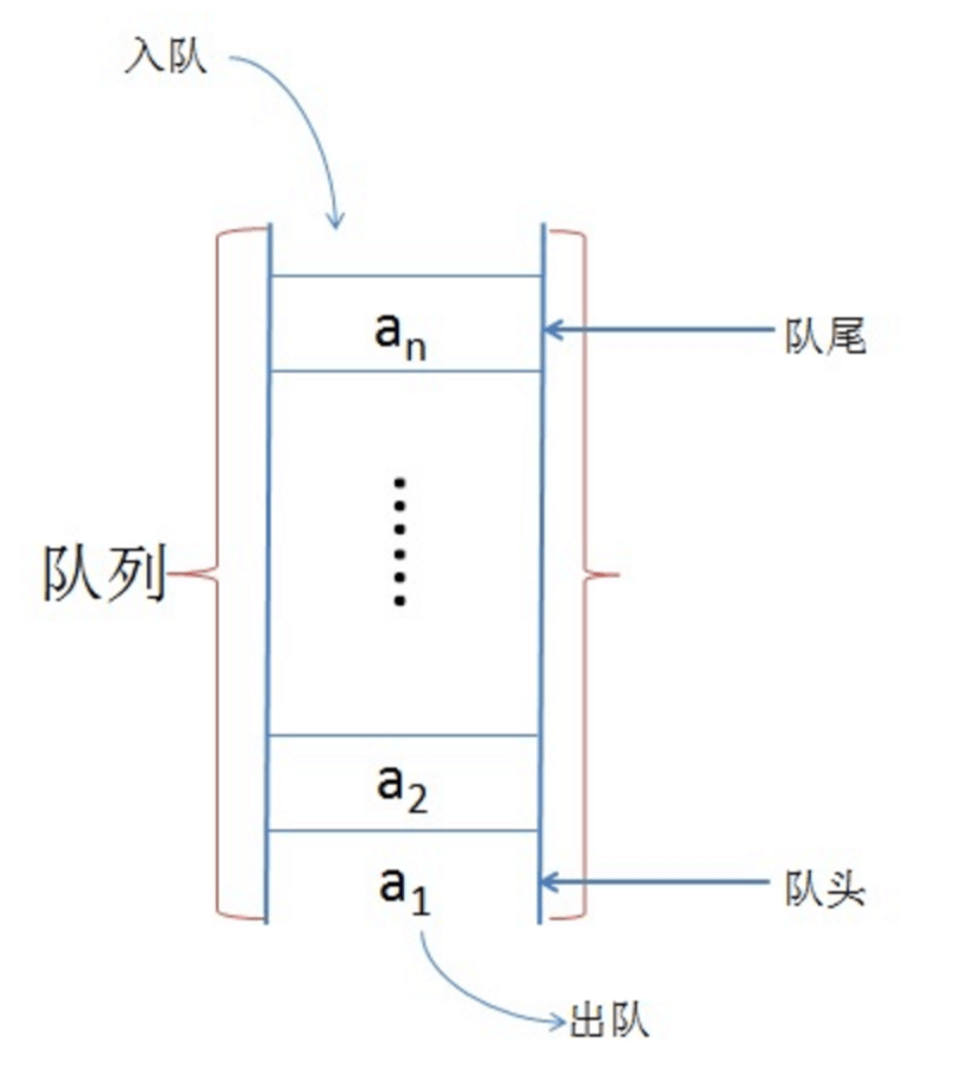
基本概念
- 向队列中添加数据叫入队
- 从队列中向外拿数据叫出队
- 队列中没有数据叫空队
- 当队列中只有1个元素的时候 该元素即是队首,又是队尾
用途:
- 消息队列、视频弹幕
- 维护打印机任务
也有一些特殊的队列,比如生活中在车站买票的时候有军人优先,这就是优先队列; 事件循环机制是一种环形队列;
# 树
树是由若干个有限节点组成的一个具有层次关系的集合。我们把它叫做“树”是因为它看起来像一棵倒挂的树。树是基本的几种数据结构之一。
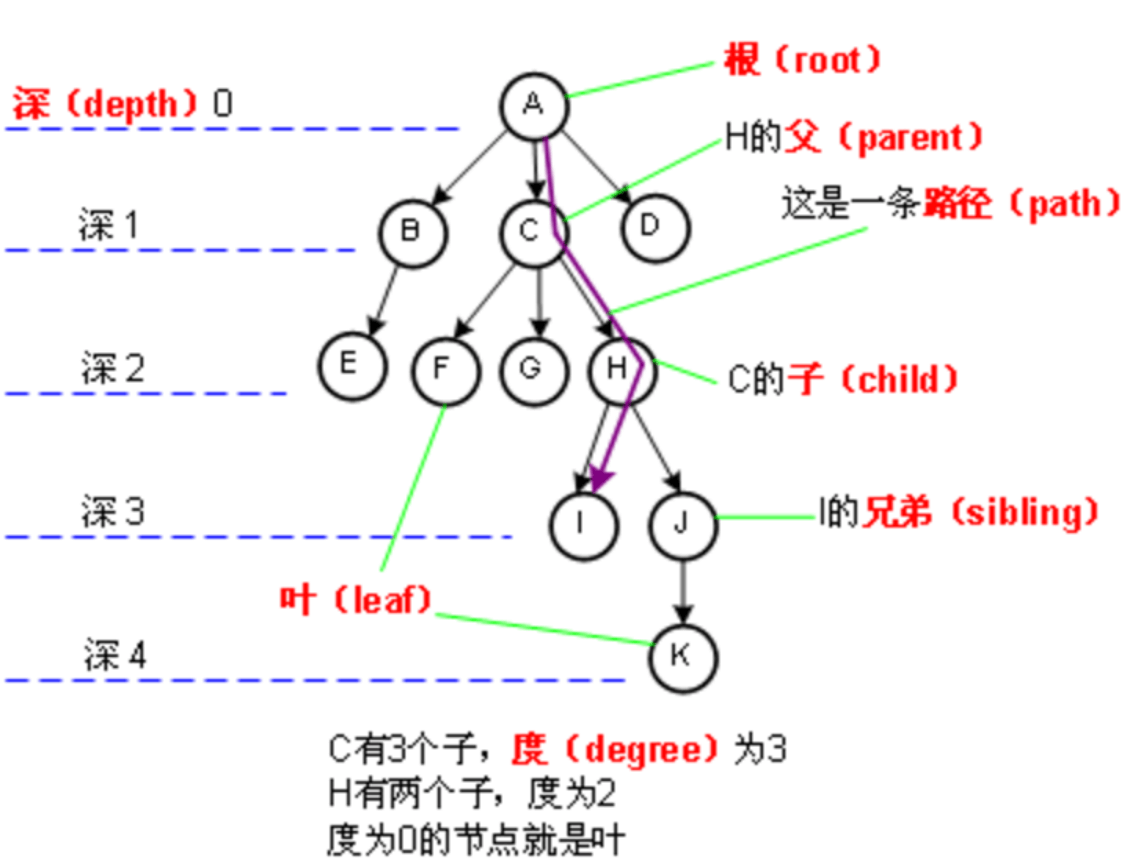
以下基本概念不如看图来的简单明了,请优先看图,或在看基本概念的时候请结合上图(树)。
主要基本概念
- 每个元素称为结点(node)
- 有一个特定的结点被称为根结点或树根(root)
- 除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树(subtree)
其余基本概念
- 单个结点是一棵树,树根就是该结点本身
- 空集合也是树,称为空树。空树中没有结点
- 一个结点含有的子树的个数称为该结点的度
- 度为0的结点称为叶结点或终端结点
- 度不为0的结点称为非终端结点或分支结点
- 若一个结点含有子结点,则这个结点称为其子结点的父结点
- 一个结点含有的子树的根结点称为该结点的子结点
- 具有相同父结点的结点互称为兄弟结点
- 一棵树中,最大的结点的度称为树的度
- 从根开始定义起,根为第1层,根的子结点为第2层,也叫深1,深2
- 树的高度或深度说的就是树中结点的最大层次
- 从根到该结点所经分支上的所有结点称为该节点的祖先
树的数学基础是:
- 图论
树的特点
- 每个结点有零个或多个子结点;
- 没有父结点的结点称为根结点;
- 每一个非根结点有且只有一个父结点;
- 除了根结点外,每个子结点可以分为多个不相交的子树;
- 一棵树中每两个点之间都有且只有一条路径
- 一颗有N个点的树有N-1条边
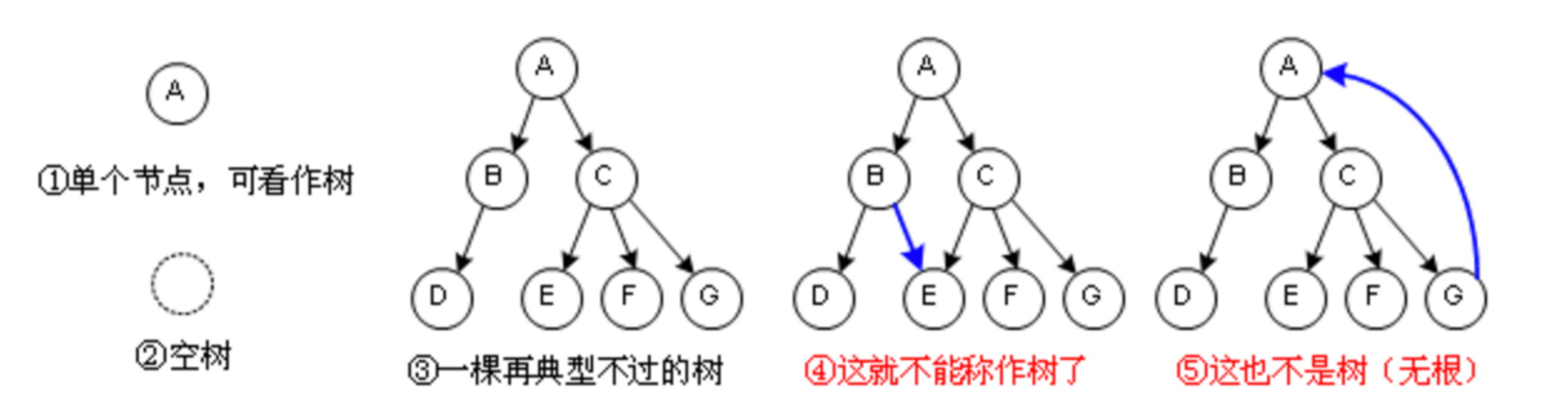
试一试
分辨下图哪一个是树:
# 树的遍历
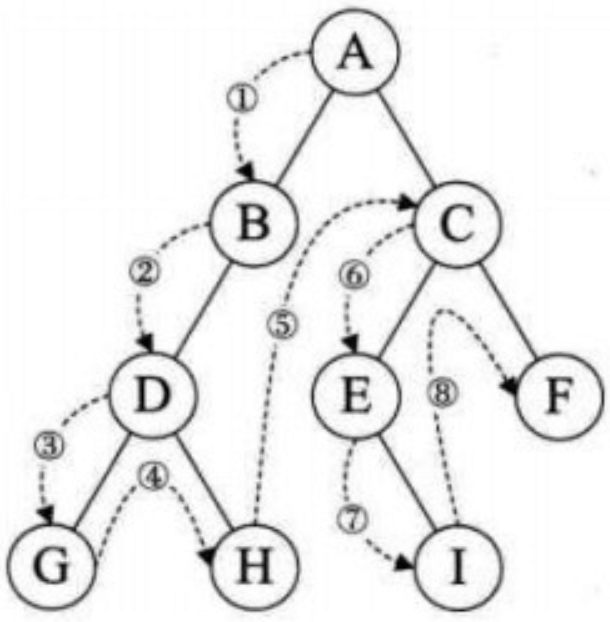
按照某种规则,不重复地访问某种树的所有节点。
先序遍历(深度优先)
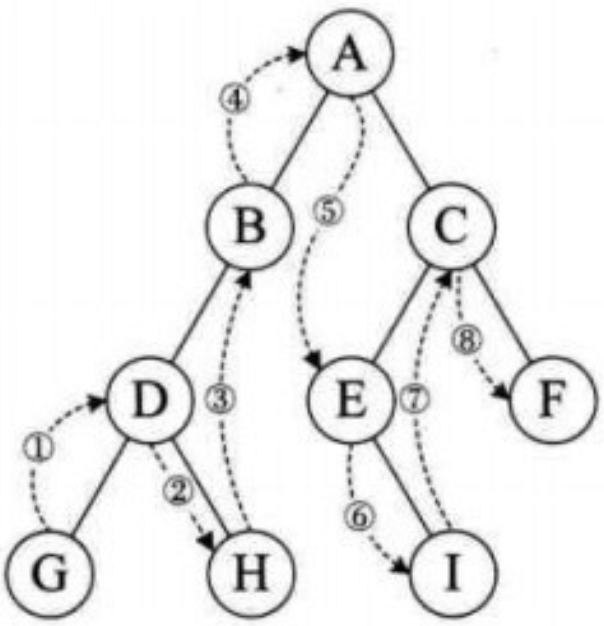
中序遍历(深度优先)
后序遍历(深度优先)
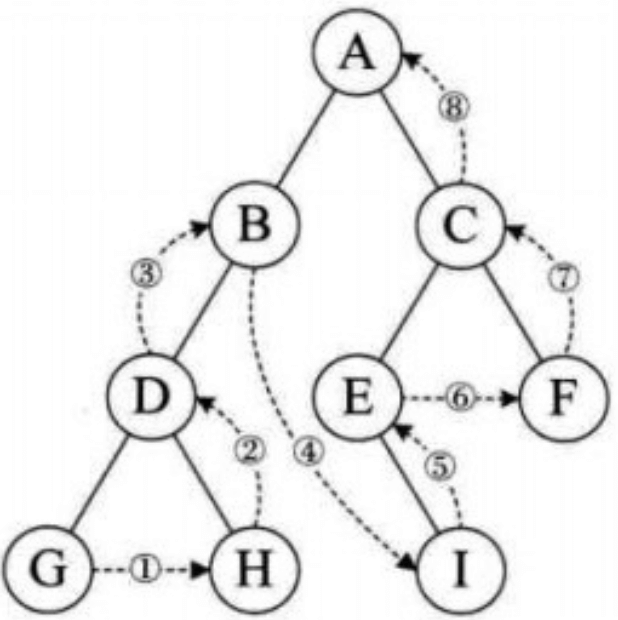
层序遍历(广度优先)
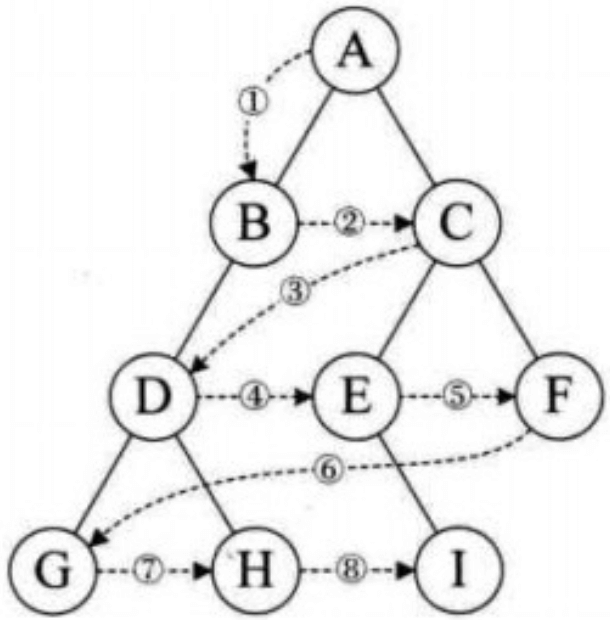
# 树的衍生
- 无序树:树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树
- 有序树:树中任意节点的子结点之间有顺序关系
- 二叉树:每个节点最多含有两个子树的树称为二叉树
- 完全二叉树:除了最后一层,其它各层节点数都达到最大
- 满二叉树:每一层上的结点数都是最大结点数
- 霍夫曼树:带权路径最短的二叉树,也叫最优二叉树
具体的可以移步Wiki或者百度百科 (^-^)
# 图
由顶点的集合(不能是空集)和边的集合组成的结构,表现的是多对多的关系
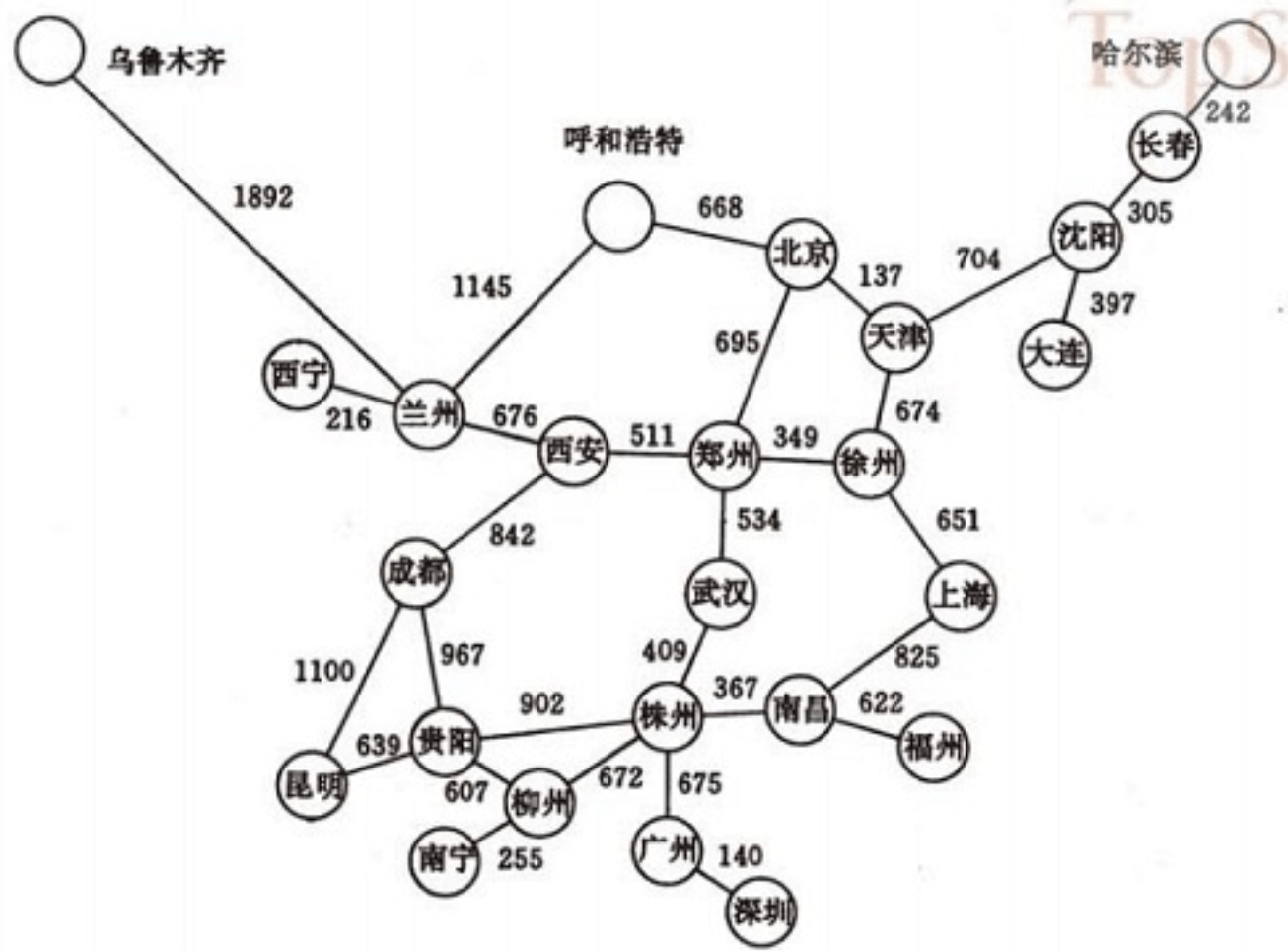
- 数学基础是:图论
- 几个基本概念:
- 顶点
- 边
- 权
- 有向图与无向图
# 前端中的数据结构应用
- 1.了解常识级别的数据结构与算法
- 2.传统前端的核心是DOM
- 3.编写自己的前端控件
- 4.前端游戏
- 5.图像处理
- ...
# 结语
到这里大家应该对于基本的数据结构有了一定的了解,算法的世界中,了解数据结构有助于我们更好的、更快的处理数据。
计算机世界的知识很多都是从现实世界中学习过来的。多了解我们的生活,也就是在了解计算机世界。
# 致谢
感谢大家阅读我的文章,如果对我感兴趣可以点击页面右上角,帮我点个star。
作者:前端小然子
链接: https://xiaoranzife.com/guide/arithmetic/0.structure.html
来源:前端小然子的博客
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
← 理解内存与指针 常用算法和复杂度小记 →